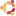-
/BogdanovBelsky_UstnySchet.jpg)
Колодец Лотоса.Задача жрецов бога РА
Теги:
Сообщение было перенесено из темы Совсем рехнулись с этими попаданцами..
Sandro> Триангуляция в современном и окончательном виде — это, пожалуй, Эйлер. С его пониманием связи между факториалом и тригонометрическими функциями. А в Древнем Египте времён строительства пирамид не умели делить произвольный угол пополам. Из-за это внутренности сложной кладки у них выглядят странно.
Вы про ложный свод? Или про что? Вообще почему-то я не помню, как в Египте занимались тригонометрией. Площадь треугольника тогда считали действительно по дурацки. Но это явно для упрощения.
С другой стороны вот эту задачу из Древнего Египта
[показать]
Сейчас аналитически мало какой школьник сможет решить
Вы про ложный свод? Или про что? Вообще почему-то я не помню, как в Египте занимались тригонометрией. Площадь треугольника тогда считали действительно по дурацки. Но это явно для упрощения.
С другой стороны вот эту задачу из Древнего Египта
[показать]
Сейчас аналитически мало какой школьник сможет решить
История "Планеты Бурь" http://shubinpavel.ru/




PSS> С другой стороны вот эту задачу из Древнего Египта
PSS> [показать]
PSS> Сейчас аналитически мало какой школьник сможет решить
В древнем ебипете тоже. Решали задачу не рядовые школьники, а кандидаты в жрецы какого-то бога. Кандидата для этого замуровывали в помещение с искомым колодцем и тростинками. В этом помещении валялись кости предыдущих кандидатов, которым не повезло. После успешного решения задачи, чувака размуровывали и он становился жрецом. Жрецы ходили лысыми, потому что в процессе решения задачи многие седели и их стригли в ноль.
Лично я щетаю, что достаточно уметь решать в уме это:
PSS> [показать]
PSS> Сейчас аналитически мало какой школьник сможет решить
В древнем ебипете тоже. Решали задачу не рядовые школьники, а кандидаты в жрецы какого-то бога. Кандидата для этого замуровывали в помещение с искомым колодцем и тростинками. В этом помещении валялись кости предыдущих кандидатов, которым не повезло. После успешного решения задачи, чувака размуровывали и он становился жрецом. Жрецы ходили лысыми, потому что в процессе решения задачи многие седели и их стригли в ноль.
Лично я щетаю, что достаточно уметь решать в уме это:


PSS>> С другой стороны вот эту задачу из Древнего Египта
TEvg-2> В древнем ебипете тоже. Решали задачу не рядовые школьники, а кандидаты в жрецы какого-то бога....
И кто ж вам с PSS про то поведал? Явно с одного и не кадемического "поседели/лысели" источника
TEvg-2> В древнем ебипете тоже. Решали задачу не рядовые школьники, а кандидаты в жрецы какого-то бога....
И кто ж вам с PSS про то поведал? Явно с одного и не кадемического "поседели/лысели" источника

Лучше других аргументов и доводов мировоззрение защищает полиция (с) С. Лем
Все самые большие глупости на свете делаются с серьезным выражением лица
Тот самый




Invar>> И кто ж вам с PSS про то поведал? Явно с одного и не кадемического "поседели/лысели" источника 
TEvg-2> Савецкие научпоп книжки класса "на суше и на море".
Тогда вернее всего "Колодец лотоса" Казанцева. А он откуда?

TEvg-2> Савецкие научпоп книжки класса "на суше и на море".
Тогда вернее всего "Колодец лотоса" Казанцева. А он откуда?
Лучше других аргументов и доводов мировоззрение защищает полиция (с) С. Лем
Все самые большие глупости на свете делаются с серьезным выражением лица
Тот самый




PSS>>> С другой стороны вот эту задачу из Древнего Египта
TEvg-2>> В древнем ебипете тоже. Решали задачу не рядовые школьники, а кандидаты в жрецы какого-то бога....
Invar> И кто ж вам с PSS про то поведал? Явно с одного и не кадемического "поседели/лысели" источника
А где у меня про лысели? У меня из "Наука и Жизнь" второй половины 80х. Там история как археолог нашел этот колодец и прочитал текст задачи выбитый рядом.
У меня из "Наука и Жизнь" второй половины 80х. Там история как археолог нашел этот колодец и прочитал текст задачи выбитый рядом.
TEvg-2>> В древнем ебипете тоже. Решали задачу не рядовые школьники, а кандидаты в жрецы какого-то бога....
Invar> И кто ж вам с PSS про то поведал? Явно с одного и не кадемического "поседели/лысели" источника

А где у меня про лысели?
 У меня из "Наука и Жизнь" второй половины 80х. Там история как археолог нашел этот колодец и прочитал текст задачи выбитый рядом.
У меня из "Наука и Жизнь" второй половины 80х. Там история как археолог нашел этот колодец и прочитал текст задачи выбитый рядом.
История "Планеты Бурь" http://shubinpavel.ru/




TEvg-2> Лично я щетаю, что достаточно уметь решать в уме это:
TEvg-2> http://upload.wikimedia.org/wikipedia/commons/a/a7/BogdanovBelsky_UstnySchet.jpg
Два. Дело в том, что тогда упоминали как курьез, что 102+112+122=132+142=365
Другими словами здесь не решение в уме а, по сути, заранее подсказка ответа
TEvg-2> http://upload.wikimedia.org/wikipedia/commons/a/a7/BogdanovBelsky_UstnySchet.jpg
Два. Дело в том, что тогда упоминали как курьез, что 102+112+122=132+142=365
Другими словами здесь не решение в уме а, по сути, заранее подсказка ответа
История "Планеты Бурь" http://shubinpavel.ru/




TEvg-2>> Савецкие научпоп книжки класса "на суше и на море".
Invar> Тогда вернее всего "Колодец лотоса" Казанцева. А он откуда?
Нашел. "Наука и Жизнь" 1966 год
Invar> Тогда вернее всего "Колодец лотоса" Казанцева. А он откуда?
Нашел. "Наука и Жизнь" 1966 год

Прикреплённые файлы:
История "Планеты Бурь" http://shubinpavel.ru/




PSS> Нашел. "Наука и Жизнь" 1966 год 
Колодец Лотоса Казанцева был впервые опубликован в сборнике «На суше и на море" 1975 года. И чует мое сердце, что Казанцев читал "Науку и жизнь"


Колодец Лотоса Казанцева был впервые опубликован в сборнике «На суше и на море" 1975 года. И чует мое сердце, что Казанцев читал "Науку и жизнь"


Александр Петрович Казанцев, Мариан Сиянин «Колодец Лотоса»
Любовь к прекрасной царице Хатшепсут приводит молодого художника к Колодцу Лотоса - место испытания жрецов Ра. Сможет ли возлюбленный великой царицы решить задачу, ответ на которую знают только сами жрецы? // fantlab.ru
Прикреплённые файлы:
История "Планеты Бурь" http://shubinpavel.ru/




PSS>> Нашел. "Наука и Жизнь" 1966 год 
PSS> Колодец Лотоса Казанцева был впервые опубликован в сборнике «На суше и на море" 1975 года.
Польский след:


PSS> Колодец Лотоса Казанцева был впервые опубликован в сборнике «На суше и на море" 1975 года.
Польский след:
Впервые с этой задачей мы ознакомились в 1966 году в январском номере журнала Наука и жизнь в рубрике «Математические досуги». Автором был указан С.Тымовский (г.Варшава). В заметке также упоминается «известный» египтолог В.Т.Детрие, который ныне на просторах Интернета совершенно не проглядывается.
Так что задача эта наша современница и родом из Польши. А то я видел статьи о божественности данной задачи
Можете сравнить решение Штейнгауза. На мой взгляд оно красивее приведенных в журнале. К тому же легко реализуется, например в Excel.
Я уверен, что автором этой задачи является Гуго Штейнгауз.

Задачи Штейнгауза :: Не решается алгебра/высшая математика?.. ПОМОЖЕМ! :: @дневники: асоциальная сеть
Здесь можно быть или не быть собой. // www.diary.ru
Лучше других аргументов и доводов мировоззрение защищает полиция (с) С. Лем
Все самые большие глупости на свете делаются с серьезным выражением лица
Тот самый




Invar> Польский след:
Возможно. Действительно возможно. Хотя было бы весомее если бы задачу нашли в сборнике выпушенном до публикации в НИЖ.
Плюс само по себе отсутствие подобного египтолого в такой транскрипции ничего не значит. Английская транскрипция из нее не очевидна, а в гугле и рунете индексированы только более менее известные египтологи. А египтология в 19 начале 20 века была очень популярна и тогда подобными исследованиями занимались все кому не лень. Причем о многих людях которые реально сделали определенный вклад в египтологию нет ни в русской или английской википедии. Сейчас для пробы попробовал найти там братьев Эдгар и не нашел. В 1906 году они прошли с фотоаппаратом по застенкам пирамиды Хеопса и сфотографировали там все. И это один из ключевых источников сейчас. Но кроме специализированных сайтов о них не пишут. Иследователей же других менее известных пирамид (которых в Египте хватает) даже на английском очень сложно найти, даже зная точно как их звали
Возможно. Действительно возможно. Хотя было бы весомее если бы задачу нашли в сборнике выпушенном до публикации в НИЖ.
Плюс само по себе отсутствие подобного египтолого в такой транскрипции ничего не значит. Английская транскрипция из нее не очевидна, а в гугле и рунете индексированы только более менее известные египтологи. А египтология в 19 начале 20 века была очень популярна и тогда подобными исследованиями занимались все кому не лень. Причем о многих людях которые реально сделали определенный вклад в египтологию нет ни в русской или английской википедии. Сейчас для пробы попробовал найти там братьев Эдгар и не нашел. В 1906 году они прошли с фотоаппаратом по застенкам пирамиды Хеопса и сфотографировали там все. И это один из ключевых источников сейчас. Но кроме специализированных сайтов о них не пишут. Иследователей же других менее известных пирамид (которых в Египте хватает) даже на английском очень сложно найти, даже зная точно как их звали
История "Планеты Бурь" http://shubinpavel.ru/




Invar>> Польский след:
PSS> Возможно. Действительно возможно. Хотя было бы весомее если бы задачу нашли в сборнике выпушенном до публикации в НИЖ.
PSS> Плюс само по себе отсутствие подобного египтолого в такой транскрипции ничего не значит.
Ага Хранцуза в инете = иголку в стоге
Хранцуза в инете = иголку в стоге 
Но аналитическое решение даёт уравнение 4 степени?
Мимо такого даже частного уже историки математики не прошли бы точно...
PSS> Возможно. Действительно возможно. Хотя было бы весомее если бы задачу нашли в сборнике выпушенном до публикации в НИЖ.
PSS> Плюс само по себе отсутствие подобного египтолого в такой транскрипции ничего не значит.
Ага
 Хранцуза в инете = иголку в стоге
Хранцуза в инете = иголку в стоге 
Но аналитическое решение даёт уравнение 4 степени?
Мимо такого даже частного уже историки математики не прошли бы точно...
Лучше других аргументов и доводов мировоззрение защищает полиция (с) С. Лем
Все самые большие глупости на свете делаются с серьезным выражением лица
Тот самый




Invar> Но аналитическое решение даёт уравнение 4 степени?
Invar> Мимо такого даже частного уже историки математики не прошли бы точно...
Так понятно, что задачу тогда решали не аналитически. Вообще тогда подход к задачам был более утилитарным, а многое уже потом сознательно накрутили.
Взять, например, великие задачи древности. Квадратуры круга, трисекции угла и удвоения куба. Везде написано так, как будто в древности эти задачи были поставлены и пару тысяч лет не могли их решить. На самом деле их в свое время поставили, относительно быстро нашли нужное решение и особо не переживали. Задачи же решены. Новый виток начался уже в средние века когда потребовали их решение только при помощи циркуля и линейки без отметок. Причем замечание про отметки очень важное, так как линейкой с отметками трисекция угла и удвоение куба делается элементарно. В древности так его и делили/удваивали.
Так и здесь, сразу понятно, что никакого аналитического решения уравнения четвертой степени тогда не было. Матаппарат совершенно не достаточный. Но очень может быть, что там было другое решение. Геометрически уже не понять,это направление с тех пор не развивалось. Но численное приближенное уже вполне можно представить. А тогда именно такое и требовалось.
Invar> Мимо такого даже частного уже историки математики не прошли бы точно...
Так понятно, что задачу тогда решали не аналитически. Вообще тогда подход к задачам был более утилитарным, а многое уже потом сознательно накрутили.
Взять, например, великие задачи древности. Квадратуры круга, трисекции угла и удвоения куба. Везде написано так, как будто в древности эти задачи были поставлены и пару тысяч лет не могли их решить. На самом деле их в свое время поставили, относительно быстро нашли нужное решение и особо не переживали. Задачи же решены. Новый виток начался уже в средние века когда потребовали их решение только при помощи циркуля и линейки без отметок. Причем замечание про отметки очень важное, так как линейкой с отметками трисекция угла и удвоение куба делается элементарно. В древности так его и делили/удваивали.
Так и здесь, сразу понятно, что никакого аналитического решения уравнения четвертой степени тогда не было. Матаппарат совершенно не достаточный. Но очень может быть, что там было другое решение. Геометрически уже не понять,это направление с тех пор не развивалось. Но численное приближенное уже вполне можно представить. А тогда именно такое и требовалось.
История "Планеты Бурь" http://shubinpavel.ru/




Invar>> ....уравнение 4 степени?
PSS> Так понятно, что задачу тогда решали не аналитически. Вообще тогда подход к задачам был более утилитарным...
А плита с зубилом для геометра ооочень спорное подспорье

И еще, автор "вольного перевода с египетского" из НиЖ тож не ищется.
PSS> Так понятно, что задачу тогда решали не аналитически. Вообще тогда подход к задачам был более утилитарным...
А плита с зубилом для геометра ооочень спорное подспорье


И еще, автор "вольного перевода с египетского" из НиЖ тож не ищется.
Лучше других аргументов и доводов мировоззрение защищает полиция (с) С. Лем
Все самые большие глупости на свете делаются с серьезным выражением лица
Тот самый




Invar> А плита с зубилом для геометра ооочень спорное подспорье 

Invar> И еще, автор "вольного перевода с египетского" из НиЖ тож не ищется.
Это да. Тоже пытался найти. При этом упомянутая история с длинной локтя уже получает определенную подтверждение. Но слабое. Судя по источникам точно его определили только в 1927 году.
Зато нашел задачу в более раннем источнике, но без привязки к Египту
Стр 203.
Оригинальная книга 1965 года
Ссылку нашел здесь

Кстати, там предложен численно-геометрический метод решения


Invar> И еще, автор "вольного перевода с египетского" из НиЖ тож не ищется.
Это да. Тоже пытался найти. При этом упомянутая история с длинной локтя уже получает определенную подтверждение. Но слабое. Судя по источникам точно его определили только в 1927 году.
Зато нашел задачу в более раннем источнике, но без привязки к Египту
Стр 203.
Оригинальная книга 1965 года
Ссылку нашел здесь

Вся механика | Это интересно | Список имен по задаче жрецов
Главные разделы: РЕШЕНИЕ ЗАДАЧИ ЖРЕЦОВ БОГА РАPriests God's RA Task Solution Как один из варантов, представляем Вам решение знаменитой задачи жрецов в комиксах в формате PPS и PPSX (MS Office 2003 и 2007). Задача, сформулированная математиками, безусловно, интересна и вошла не только в учебники и задачники по математике (например Daniel D. McCracken, William S. Dorn: Numerical Methods and Fortran Programming, 1965; русский перевод: Д. Мак-Кракен, У. Дорн Численные методы и программирование на фортране. // Дальше — www.allmechanics.narod.ruКстати, там предложен численно-геометрический метод решения
История "Планеты Бурь" http://shubinpavel.ru/




Это сообщение редактировалось 08.01.2018 в 10:26
Сообщение было перенесено из темы Совсем рехнулись с этими попаданцами..
Насчёт задачи с колодцем. Есть и более простой способ решения.
Перенести плоскость задачи с размерами на пол или стену - т.е. перейти к измерению размера по масштабному чертежу.
Египтяне сложные инженерные задачи решали скорее всего аналоговыми методами.
Перенести плоскость задачи с размерами на пол или стену - т.е. перейти к измерению размера по масштабному чертежу.
Египтяне сложные инженерные задачи решали скорее всего аналоговыми методами.



Это сообщение редактировалось 08.01.2018 в 07:31
- PSS [08.01.2018 10:03]: Тема создана из Совсем рехнулись с этими попаданцами.
- PSS [08.01.2018 10:10]: Перенос сообщений из Совсем рехнулись с этими попаданцами.
Дем> Тупо откладываем диаметр колодца N раз, пока он не даст целое число мер.
Дем> Получаем как понимаю 16/13
Не всегда есть решение в виде дроби с малыми числами, может оказаться 253/274, например. Откладываем мерную единицу разумное количество раз и измеряемый предмет, находим лучшее совпадение (по принципу шкалы нониуса).
Дем> Получаем как понимаю 16/13
Не всегда есть решение в виде дроби с малыми числами, может оказаться 253/274, например. Откладываем мерную единицу разумное количество раз и измеряемый предмет, находим лучшее совпадение (по принципу шкалы нониуса).


- Последние действия над темой
- PSS [08.01.2018 10:03]: Тема создана из Совсем рехнулись с этими попаданцами.
- PSS [08.01.2018 10:10]: Перенос сообщений из Совсем рехнулись с этими попаданцами.
- Все действия над темой
Copyright © Balancer 1997..2018
Создано 05.01.2018
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
Создано 05.01.2018
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
- Поиск
- Настройки
-
- Персональное
-
Здравствуйте, гость!
Гостевой функционал сайта ограничен. Для полноценной работы зарегистрируйтесь, пожалуйста.
- Тема
- RPG (самоуправление)
- Твиттер сайта Твиты пользователя @AirbaseRu
- Статистика
 PSS
PSS

 инфо
инфо инструменты
инструменты

 Invar
Invar





 digger
digger