-
/primordial-earth-crash-armageddon-doom.jpg)
Научно-техническая обоснованность возможности полётов к звёздам
Теги:
s.t.> Да чего умного то, с межпланетными полетами в начале века все было ясно - они возможны, мы их наблюдали, а один перелетчик даже грохнулся в Сибири.
"Марсианские" метеориты - совсем недавняя находка.
Во времена Жюль Верна "естественные" межпланетные перелеты известны не были.
"Марсианские" метеориты - совсем недавняя находка.
Во времена Жюль Верна "естественные" межпланетные перелеты известны не были.


PSS> Де юре нельзя. На это требовались очень большие ресурсы. Так как такие расчеты требуют значительных человекочасов. Тогда еле еле посчитали комету Галлея.
Когда появились логарифмические линейки современного (ну, т.е. уже уровня прошлого века, конечно) вида? На ней можно довольно быстро расчитать приблизительную траекторию с 2-3 значной точностью. Для реального полёта не хватит, конечно, а чтобы понять вид траектории — хватит.
Повторюсь, спор не о том, можно ли было слетать на Луну при Жюле Верне. Нельзя. Спор о том, можно ли было тогда понять, как нужно лететь. Можно.
Когда появились логарифмические линейки современного (ну, т.е. уже уровня прошлого века, конечно) вида? На ней можно довольно быстро расчитать приблизительную траекторию с 2-3 значной точностью. Для реального полёта не хватит, конечно, а чтобы понять вид траектории — хватит.
Повторюсь, спор не о том, можно ли было слетать на Луну при Жюле Верне. Нельзя. Спор о том, можно ли было тогда понять, как нужно лететь. Можно.


Balancer> Повторюсь, спор не о том, можно ли было слетать на Луну при Жюле Верне. Нельзя. Спор о том, можно ли было тогда понять, как нужно лететь. Можно.
...спор не о том, можно ли было слетать на Проксима Центавру при Балансере. Нельзя. Спор о том, можно ли было тогда понять, как нужно лететь. Можно.

...спор не о том, можно ли было слетать на Проксима Центавру при Балансере. Нельзя. Спор о том, можно ли было тогда понять, как нужно лететь. Можно.



Это сообщение редактировалось 07.12.2017 в 09:06
- Balancer [07.12.2017 09:05]: Тема создана из Технологический уровень Землян, необходимый для отражения вторжения пришельцев.
Balancer> Когда появились логарифмические линейки современного (ну, т.е. уже уровня прошлого века, конечно) вида? На ней можно довольно быстро расчитать приблизительную траекторию с 2-3 значной точностью. Для реального полёта не хватит, конечно, а чтобы понять вид траектории — хватит.
Увы нельзя. Никак. Там задача решается только численно. С большим количеством итераций. Иначе бы Вернер фон Браун не рисовал и в 50е полет на Луну по методу Жуль Верна.
Balancer> Повторюсь, спор не о том, можно ли было слетать на Луну при Жюле Верне. Нельзя. Спор о том, можно ли было тогда понять, как нужно лететь. Можно.
Можно. Но явно не представляете цену этого знания. Для этого, в середине 19 века нужно было набрать несколько сотен математиков, с десяток астрономов и запереть их на полгода для проведения всех расчетов. Минимум. Для определения примерного вида траектории. Точный расчет занял бы пару лет.Причем логарифмические линейки здесь не помогут. А массовых арифмометров тогда не было. То есть только счеты и листки бумаги. Кстати и подобные фабрики расчетов насколько я помню массово появились только в начале двадцатого века.
И тогда, да, можно было бы определить траекторию еще не только в девятнадцатом веке, но и восемнадцатом! Но сами оцените реальность этого события. И сколько бы оно стоило.
Увы нельзя. Никак. Там задача решается только численно. С большим количеством итераций. Иначе бы Вернер фон Браун не рисовал и в 50е полет на Луну по методу Жуль Верна.
Balancer> Повторюсь, спор не о том, можно ли было слетать на Луну при Жюле Верне. Нельзя. Спор о том, можно ли было тогда понять, как нужно лететь. Можно.
Можно. Но явно не представляете цену этого знания. Для этого, в середине 19 века нужно было набрать несколько сотен математиков, с десяток астрономов и запереть их на полгода для проведения всех расчетов. Минимум. Для определения примерного вида траектории. Точный расчет занял бы пару лет.Причем логарифмические линейки здесь не помогут. А массовых арифмометров тогда не было. То есть только счеты и листки бумаги. Кстати и подобные фабрики расчетов насколько я помню массово появились только в начале двадцатого века.
И тогда, да, можно было бы определить траекторию еще не только в девятнадцатом веке, но и восемнадцатом! Но сами оцените реальность этого события. И сколько бы оно стоило.
История "Планеты Бурь" http://shubinpavel.ru/




PSS> Увы нельзя. Никак. Там задача решается только численно. С большим количеством итераций.
Так о чём и речь. Знаешь, сколько я этих графиков полётов строил, когда в детстве в «Лунолёт-3» играл? Так что знаю я эти расчёты... Также считал много и на логарифмической линейке до появления программируемого калькулятора. Полагаю, что замена калькулятора на логарифмическую линейку замедлит расчёты порядка на два. Т.е. вместо получаса, скажем, получится одна рабочая неделя расчётов. Вполне реальная цифра для энтузиаста
Так что знаю я эти расчёты... Также считал много и на логарифмической линейке до появления программируемого калькулятора. Полагаю, что замена калькулятора на логарифмическую линейку замедлит расчёты порядка на два. Т.е. вместо получаса, скажем, получится одна рабочая неделя расчётов. Вполне реальная цифра для энтузиаста 
PSS> Иначе бы Вернер фон Браун не рисовал и в 50е полет на Луну по методу Жуль Верна.
Или у него были более важные занятия, чем делать такой расчёт
PSS> Можно. Но явно не представляете цену этого знания. Для этого, в середине 19 века нужно было набрать несколько сотен математиков, с десяток астрономов и запереть их на полгода для проведения всех расчетов. Минимум.
Я свою оценку выше привёл При чём в расчётах там нет никаких сакральных данных, только закон притяжения, законы Ньютона и численное дифференцирование.
При чём в расчётах там нет никаких сакральных данных, только закон притяжения, законы Ньютона и численное дифференцирование.
PSS> Причем логарифмические линейки здесь не помогут. А массовых арифмометров тогда не было.
Арифмометр тут, как раз, не подойдёт. На нём будет точнее, но намного дольше. Логарифм, квадратный корень или квадрат на линейке получаются одним движением. А на арифмеметре сотнями оборотов ручки
PSS> И тогда, да, можно было бы определить траекторию еще не только в девятнадцатом веке, но и восемнадцатом!
Если в 18-м были логарифмические линейки Вручную это бы заняло на много-много порядков больше времени. По таблицам — тоже, хотя бы на 1-2 порядка. Но линейка реально очень быстрый инструмент, сравнимый с калькуляторами.
Вручную это бы заняло на много-много порядков больше времени. По таблицам — тоже, хотя бы на 1-2 порядка. Но линейка реально очень быстрый инструмент, сравнимый с калькуляторами.
...
Ага:
То есть фактически грубый расчёт траектории можно было сделать с середины XVII века. Бегунок, который в XIX появился, тут бы сильно не помог, т.к. нужно результаты операций складывать, линейка это не умеет, поэтому промежуточные точки придётся складывать на бумаге.
Так о чём и речь. Знаешь, сколько я этих графиков полётов строил, когда в детстве в «Лунолёт-3» играл?
 Так что знаю я эти расчёты... Также считал много и на логарифмической линейке до появления программируемого калькулятора. Полагаю, что замена калькулятора на логарифмическую линейку замедлит расчёты порядка на два. Т.е. вместо получаса, скажем, получится одна рабочая неделя расчётов. Вполне реальная цифра для энтузиаста
Так что знаю я эти расчёты... Также считал много и на логарифмической линейке до появления программируемого калькулятора. Полагаю, что замена калькулятора на логарифмическую линейку замедлит расчёты порядка на два. Т.е. вместо получаса, скажем, получится одна рабочая неделя расчётов. Вполне реальная цифра для энтузиаста 
PSS> Иначе бы Вернер фон Браун не рисовал и в 50е полет на Луну по методу Жуль Верна.
Или у него были более важные занятия, чем делать такой расчёт

PSS> Можно. Но явно не представляете цену этого знания. Для этого, в середине 19 века нужно было набрать несколько сотен математиков, с десяток астрономов и запереть их на полгода для проведения всех расчетов. Минимум.
Я свою оценку выше привёл
 При чём в расчётах там нет никаких сакральных данных, только закон притяжения, законы Ньютона и численное дифференцирование.
При чём в расчётах там нет никаких сакральных данных, только закон притяжения, законы Ньютона и численное дифференцирование.PSS> Причем логарифмические линейки здесь не помогут. А массовых арифмометров тогда не было.
Арифмометр тут, как раз, не подойдёт. На нём будет точнее, но намного дольше. Логарифм, квадратный корень или квадрат на линейке получаются одним движением. А на арифмеметре сотнями оборотов ручки

PSS> И тогда, да, можно было бы определить траекторию еще не только в девятнадцатом веке, но и восемнадцатом!
Если в 18-м были логарифмические линейки
 Вручную это бы заняло на много-много порядков больше времени. По таблицам — тоже, хотя бы на 1-2 порядка. Но линейка реально очень быстрый инструмент, сравнимый с калькуляторами.
Вручную это бы заняло на много-много порядков больше времени. По таблицам — тоже, хотя бы на 1-2 порядка. Но линейка реально очень быстрый инструмент, сравнимый с калькуляторами....
Ага:
Дальнейшие усовершенствования сводились к появлению второй подвижной линейки-«движка» (Роберт Биссакер, 1654 и Сет Патридж, 1657), разметке обеих сторон линейки (тоже Биссакер), добавление двух «шкал Уингейта», отметке на шкалах часто используемых чисел (Томас Эверард, 1683). Бегунок появился в середине XIX века (А. Мангейм).
То есть фактически грубый расчёт траектории можно было сделать с середины XVII века. Бегунок, который в XIX появился, тут бы сильно не помог, т.к. нужно результаты операций складывать, линейка это не умеет, поэтому промежуточные точки придётся складывать на бумаге.


Balancer> Так о чём и речь. Знаешь, сколько я этих графиков полётов строил, когда в детстве в «Лунолёт-3» играл?  Так что знаю я эти расчёты...
Так что знаю я эти расчёты...
Хм. А Вы понимаете что лунолет стоял на программируемом калькуляторе, который был мощнее первых ЭВМ? И подобных расчетных фабрик начала века?
Balancer>Также считал много и на логарифмической линейке
Без калькулятора? Не верю. Ну или как и Жуль Верн решили, что знаете траекторию, хотя в реальности она была очень далека от реальности. Вы просто не представляете схему задачи. Честно. Без обид. Траектория там, при небольших скоростях, очень зависит от точности вычислений. Даже при шаге в секунду может накопиться (и накопиться) ошибка которая покажет невозможную траекторию, с маленькой скоростью.
PSS>> Иначе бы Вернер фон Браун не рисовал и в 50е полет на Луну по методу Жуль Верна.
Balancer> Или у него были более важные занятия, чем делать такой расчёт
Тогда давайте следующий шаг. Давайте признаем, что Цандер, Годдард, Штернфельд, Оберт, Макс Валье и многие другие, когда писали свои книги про космические полеты и полеты на Луну, были заняты более важными делами, чем расчеты траекторий полета к Луне.
Balancer> Я свою оценку выше привёл При чём в расчётах там нет никаких сакральных данных, только закон притяжения, законы Ньютона и численное дифференцирование.
При чём в расчётах там нет никаких сакральных данных, только закон притяжения, законы Ньютона и численное дифференцирование.
С очень небольшим шагом и очень неустойчивое.
Balancer> Арифмометр тут, как раз, не подойдёт. На нём будет точнее, но намного дольше. Логарифм, квадратный корень или квадрат на линейке получаются одним движением. А на арифмеметре сотнями оборотов ручки
Арифмометр в численных методах обязателен. Почему, по вашему, совершенно все, с обоих сторон шарика, когда вспоминают про численные расчеты упоминают про механические мерседесы? Да просто потому, что для численных методов, при сотнях итераций, важна точность. Без нее можно вообще ничего не считать. Так как гарантировано будет вранье не имеющее смысла.
Balancer> То есть фактически грубый расчёт траектории можно было сделать с середины XVII века. Бегунок, который в XIX появился, тут бы сильно не помог, т.к. нужно результаты операций складывать, линейка это не умеет, поэтому промежуточные точки придётся складывать на бумаге.
Ну получили бы на этом грубом расчете как раз схему захвата, при низкой скорости, что рисовал Жуль Верн.
Блин. Сейчас жалею, что не показал ложные траектории которые получаются даже при точном расчете, но с небольшим шагом. Надеюсь хоть таблица покажет.
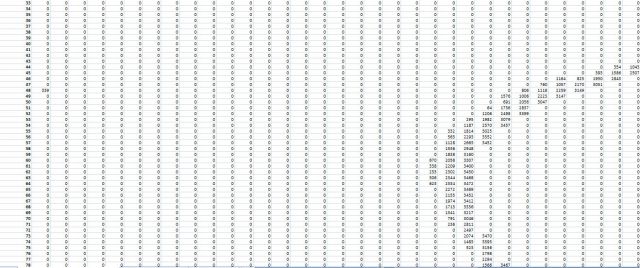
Смотрите. Нас скриншоте ниже я забивал в Эксель траектории полета на Луну, в плоскости Луны, в зависимости от шага.Здесь отображены отклонения при попадании в Луну. Ноль- станция не попала. Цифра - отклонение от центра Луны.
Шаг одна секунда. Значит итераций 363 тысячи. И достаточная точность вычислений.
Видите слева есть цифра - 339. То есть станция попала в Луну. При этом отметка находиться заметно левее конца реальной кривой траекторий, которые означают попадание в Луну. И значит это ложь. Которая вылезла о даже при таких данных.
Там получаются очень низкие скорости, в вершине траектории, и возмущения на следующем шаге будут значительными и приводит к такому фиктивному попаданию в Луну. И такие точки находятся на скоростях в сотни метров в секунду ниже реальных и при оценке минимальной траектории, при низком расчете на них попадут в первую очередь.
Что самое удивительное, именно эти точки выглядят как траектории Жуль Верна. Захват на подлете. И при меньшей точности вычислений, с итерациями, они лезут постоянно. Даже при численных методах и вычислении на ЭВМ. При худщей точности был бы вообще кошмар При этом сейчас точно известно, что захват Луной на первом витке невозможен.
Так что это ошибка. Которую, при низкой точности расчетом можно принять за реальность. Убедившись, что Жуль Верн был прав.
Более того, к моему удивлению, именно для пушечной схемы такие ошибочные расчеты наиболее часто вылазят. Из-за схемы полета. Старт с орбиты Земли более стабилен.
 Так что знаю я эти расчёты...
Так что знаю я эти расчёты... Хм. А Вы понимаете что лунолет стоял на программируемом калькуляторе, который был мощнее первых ЭВМ? И подобных расчетных фабрик начала века?
Balancer>Также считал много и на логарифмической линейке
Без калькулятора? Не верю. Ну или как и Жуль Верн решили, что знаете траекторию, хотя в реальности она была очень далека от реальности. Вы просто не представляете схему задачи. Честно. Без обид. Траектория там, при небольших скоростях, очень зависит от точности вычислений. Даже при шаге в секунду может накопиться (и накопиться) ошибка которая покажет невозможную траекторию, с маленькой скоростью.
PSS>> Иначе бы Вернер фон Браун не рисовал и в 50е полет на Луну по методу Жуль Верна.
Balancer> Или у него были более важные занятия, чем делать такой расчёт

Тогда давайте следующий шаг. Давайте признаем, что Цандер, Годдард, Штернфельд, Оберт, Макс Валье и многие другие, когда писали свои книги про космические полеты и полеты на Луну, были заняты более важными делами, чем расчеты траекторий полета к Луне.
Balancer> Я свою оценку выше привёл
 При чём в расчётах там нет никаких сакральных данных, только закон притяжения, законы Ньютона и численное дифференцирование.
При чём в расчётах там нет никаких сакральных данных, только закон притяжения, законы Ньютона и численное дифференцирование.С очень небольшим шагом и очень неустойчивое.
Balancer> Арифмометр тут, как раз, не подойдёт. На нём будет точнее, но намного дольше. Логарифм, квадратный корень или квадрат на линейке получаются одним движением. А на арифмеметре сотнями оборотов ручки

Арифмометр в численных методах обязателен. Почему, по вашему, совершенно все, с обоих сторон шарика, когда вспоминают про численные расчеты упоминают про механические мерседесы? Да просто потому, что для численных методов, при сотнях итераций, важна точность. Без нее можно вообще ничего не считать. Так как гарантировано будет вранье не имеющее смысла.
Balancer> То есть фактически грубый расчёт траектории можно было сделать с середины XVII века. Бегунок, который в XIX появился, тут бы сильно не помог, т.к. нужно результаты операций складывать, линейка это не умеет, поэтому промежуточные точки придётся складывать на бумаге.
Ну получили бы на этом грубом расчете как раз схему захвата, при низкой скорости, что рисовал Жуль Верн.
Блин. Сейчас жалею, что не показал ложные траектории которые получаются даже при точном расчете, но с небольшим шагом. Надеюсь хоть таблица покажет.
Смотрите. Нас скриншоте ниже я забивал в Эксель траектории полета на Луну, в плоскости Луны, в зависимости от шага.Здесь отображены отклонения при попадании в Луну. Ноль- станция не попала. Цифра - отклонение от центра Луны.
Шаг одна секунда. Значит итераций 363 тысячи. И достаточная точность вычислений.
Видите слева есть цифра - 339. То есть станция попала в Луну. При этом отметка находиться заметно левее конца реальной кривой траекторий, которые означают попадание в Луну. И значит это ложь. Которая вылезла о даже при таких данных.
Там получаются очень низкие скорости, в вершине траектории, и возмущения на следующем шаге будут значительными и приводит к такому фиктивному попаданию в Луну. И такие точки находятся на скоростях в сотни метров в секунду ниже реальных и при оценке минимальной траектории, при низком расчете на них попадут в первую очередь.
Что самое удивительное, именно эти точки выглядят как траектории Жуль Верна. Захват на подлете. И при меньшей точности вычислений, с итерациями, они лезут постоянно. Даже при численных методах и вычислении на ЭВМ. При худщей точности был бы вообще кошмар При этом сейчас точно известно, что захват Луной на первом витке невозможен.
Так что это ошибка. Которую, при низкой точности расчетом можно принять за реальность. Убедившись, что Жуль Верн был прав.
Более того, к моему удивлению, именно для пушечной схемы такие ошибочные расчеты наиболее часто вылазят. Из-за схемы полета. Старт с орбиты Земли более стабилен.
Прикреплённые файлы:
История "Планеты Бурь" http://shubinpavel.ru/




PSS> Более того, к моему удивлению, именно для пушечной схемы такие ошибочные расчеты наиболее часто вылазят. Из-за схемы полета. Старт с орбиты Земли более стабилен.
О! Нашел. Здесь, для интереса, с небольшим (для современных ЭВМ) шагом просчитал именно пушечный полет на Луну вертикально верх. Для разной начальной скорости и отклонения Луны от направления "выстрела"
На графике цветом обозначены дальность пролета от центра Луны. Кривая в верхнем правом углу как раз кривая попадания в Луну.
Вот и сами оцените что получается когда снаряд подлетает к вершине траектории с нулевой скоростью. А на него действуют гравитации Луны и Земли. И сколько там вылазиет "мусора". Включая фиктивные попадания в Луну при небольших скоростях. Причем по невозможной траектории захвата.
И именно это было бы с логарифмическими линейками. Или даже арифмометрами с небольшим шагом. Получили бы невозможную траекторию захвата с малой скоростью и были бы уверены, что решили задачу попадания в Луну. Если бы вдруг запустили снаряд с такой скоростью, то очень бы удивились. Он бы даже до сферы действия Луны не долетел бы.
О! Нашел. Здесь, для интереса, с небольшим (для современных ЭВМ) шагом просчитал именно пушечный полет на Луну вертикально верх. Для разной начальной скорости и отклонения Луны от направления "выстрела"
На графике цветом обозначены дальность пролета от центра Луны. Кривая в верхнем правом углу как раз кривая попадания в Луну.
Вот и сами оцените что получается когда снаряд подлетает к вершине траектории с нулевой скоростью. А на него действуют гравитации Луны и Земли. И сколько там вылазиет "мусора". Включая фиктивные попадания в Луну при небольших скоростях. Причем по невозможной траектории захвата.
И именно это было бы с логарифмическими линейками. Или даже арифмометрами с небольшим шагом. Получили бы невозможную траекторию захвата с малой скоростью и были бы уверены, что решили задачу попадания в Луну. Если бы вдруг запустили снаряд с такой скоростью, то очень бы удивились. Он бы даже до сферы действия Луны не долетел бы.
Прикреплённые файлы:
История "Планеты Бурь" http://shubinpavel.ru/




ttt>> Что полет возможен вообще сейчас очевидно.
s.t.> Очевидно как раз обратное. Смотри выше.
Зачем выше смотреть? Эта тема полно где муссируется. Мы же говорим не об ОРГАНИЗАЦИИ межзвездного полета, а о его возможности. Если совершенно серьезно обсуждается посылка зонда (граммового пусть) к звездам, то уж принципиальная возможность полета человека очевидна. Когда и как еще непонятно да.
s.t.> Очевидно как раз обратное. Смотри выше.
Зачем выше смотреть? Эта тема полно где муссируется. Мы же говорим не об ОРГАНИЗАЦИИ межзвездного полета, а о его возможности. Если совершенно серьезно обсуждается посылка зонда (граммового пусть) к звездам, то уж принципиальная возможность полета человека очевидна. Когда и как еще непонятно да.
http://tl2002.livejournal.com/




Прошлая диаграмма в перспективе. Траектория попадания, конечно, внизу. Куда сходиться овраг
Прикреплённые файлы:
История "Планеты Бурь" http://shubinpavel.ru/




Fakir>> Гораздо хуже. Флогистон объяснял реально наблюдаемые явления.
U235> И не просто описывал, а позволял посчитать. Приличная часть и поныне используемых формул термодинамики и используемых понятий, типа теплоемкости и количества теплоты введены в рамках теории флогистона.
Не надо фигни и путать флогистон с теплородом.
Флогистон количественных теорий вообще не давал.
U235> И не просто описывал, а позволял посчитать. Приличная часть и поныне используемых формул термодинамики и используемых понятий, типа теплоемкости и количества теплоты введены в рамках теории флогистона.
Не надо фигни и путать флогистон с теплородом.
Флогистон количественных теорий вообще не давал.


Полл>> А в наше время "Вояджер" улетел чуть-чуть дальше Луны.
Balancer> Ну, всё равно, если в масштабе Вайверна люди летали на 3 см. от Земли, то Вояджер улетел на 100 метров.
На самом деле метров на 500-600 НО! Это не человек и улетел он, честно говоря, случайно
НО! Это не человек и улетел он, честно говоря, случайно 
Balancer> Ну, всё равно, если в масштабе Вайверна люди летали на 3 см. от Земли, то Вояджер улетел на 100 метров.
На самом деле метров на 500-600
 НО! Это не человек и улетел он, честно говоря, случайно
НО! Это не человек и улетел он, честно говоря, случайно 
Жизнь коротка, путь искусства долог, удобный случай мимолетен, опыт обманчив.... Ἱπποκράτης




Cormorant> Это все яйца в одной корзине.
потому и нужна экспансия в космос... К спору о том, зачем она.
потому и нужна экспансия в космос... К спору о том, зачем она.
Voeneuch, учи физику, манажор ))




Полл>
http://static3.businessinsider.com/image/528226bd6bb3f7ba0ed7df63-1200-924/primordial-earth-crash-armageddon-doom.jpg
Полл> Экосфера, кстати, после подобного инцидента уцелеет. Так что планета останется пригодной для жизни. Для любителей объяснять вторжение алиенов комфортными условиями Земли.
Кстати, у меня была совсем другая картинка для именно, что геноцида землян
Где то в поясе астероидов оккупанты собирают гигантский гаусс на сверхпроводящих кольцах и наносят удар по городам - согласно карте вечернего свечения Земли - мегатонн по 50 каждый выстрел (на 3% от с это снарядик в несколько тонн). Вечером тех же суток высаживают дронов с программой отстрела двуногих (гориллам и шимпанзе мои соболезнования). Через годик - приходи, заселяйся...
http://static3.businessinsider.com/image/528226bd6bb3f7ba0ed7df63-1200-924/primordial-earth-crash-armageddon-doom.jpg
Полл> Экосфера, кстати, после подобного инцидента уцелеет. Так что планета останется пригодной для жизни. Для любителей объяснять вторжение алиенов комфортными условиями Земли.
Кстати, у меня была совсем другая картинка для именно, что геноцида землян

Где то в поясе астероидов оккупанты собирают гигантский гаусс на сверхпроводящих кольцах и наносят удар по городам - согласно карте вечернего свечения Земли - мегатонн по 50 каждый выстрел (на 3% от с это снарядик в несколько тонн). Вечером тех же суток высаживают дронов с программой отстрела двуногих (гориллам и шимпанзе мои соболезнования). Через годик - приходи, заселяйся...
Жизнь коротка, путь искусства долог, удобный случай мимолетен, опыт обманчив.... Ἱπποκράτης




Wyvern-2> Кстати, у меня была совсем другая картинка для именно, что геноцида землян
Собирать "гигантский гаусс"... Составлять карту городов... Бить прицельно по городам... Еще дронов потом штамповать и доставлять на поверхность...
"Добрыня Никитич, обсыпь этого придурка мелом и дай мне мою булаву" (© Илья Муромец из анекдота в ответ на крестик мелом, нарисованный на нем д`Артаньяном.)
Собирать "гигантский гаусс"... Составлять карту городов... Бить прицельно по городам... Еще дронов потом штамповать и доставлять на поверхность...
"Добрыня Никитич, обсыпь этого придурка мелом и дай мне мою булаву" (© Илья Муромец из анекдота в ответ на крестик мелом, нарисованный на нем д`Артаньяном.)


PSS> Хм. А Вы понимаете что лунолет стоял на программируемом калькуляторе
Прекрасно понимаю.
PSS> Без калькулятора? Не верю.
Это Ваши проблемы
PSS> Ну или как и Жуль Верн решили, что знаете траекторию, хотя в реальности она была очень далека от реальности.
Я с самого начала отметил, что речь не о точной, а о приближённой траектории.
PSS> Вы просто не представляете схему задачи. Честно. Без обид.
Я не просто представляю себе задачу. Я решал её многие десятки раз. В отличие от Вас, видимо. Без обид.
Прекрасно понимаю.
PSS> Без калькулятора? Не верю.
Это Ваши проблемы

PSS> Ну или как и Жуль Верн решили, что знаете траекторию, хотя в реальности она была очень далека от реальности.
Я с самого начала отметил, что речь не о точной, а о приближённой траектории.
PSS> Вы просто не представляете схему задачи. Честно. Без обид.
Я не просто представляю себе задачу. Я решал её многие десятки раз. В отличие от Вас, видимо. Без обид.


PSS>> Ну или как и Жуль Верн решили, что знаете траекторию, хотя в реальности она была очень далека от реальности.
Balancer> Я с самого начала отметил, что речь не о точной, а о приближённой траектории.
Которая принципиально будет не верной. И в реальности станция полетит по совсем другой траектории
В этом случае и Жуль Верн оценил приближенную траекторию. Кому интересно, что по ней на Луну не долететь?
Balancer> Я не просто представляю себе задачу. Я решал её многие десятки раз. В отличие от Вас, видимо. Без обид.
Ик. То есть я тут схемы от генератора случайных чисел выкладываю? Это что вообще было??
Это что вообще было??
Что до решения задачи. И станции запускали? Хотя бы виртуально? Скажем, моделируя траекторию реальной станции, вроде "Луны-3". Для проверки? Если скажете, что так и было. И в реальности повторили траекторию "Луны-3" (или другой станции) только при помощи логарифмической линейки, и результатсошелся с опубликованными данными, то я действительно поверю, что расчет только на линейке возможен. Хотя и очень удивлюсь. Вы даже не представите насколько.
Balancer> Я с самого начала отметил, что речь не о точной, а о приближённой траектории.
Которая принципиально будет не верной. И в реальности станция полетит по совсем другой траектории

В этом случае и Жуль Верн оценил приближенную траекторию. Кому интересно, что по ней на Луну не долететь?
Balancer> Я не просто представляю себе задачу. Я решал её многие десятки раз. В отличие от Вас, видимо. Без обид.
Ик. То есть я тут схемы от генератора случайных чисел выкладываю?
 Это что вообще было??
Это что вообще было??Что до решения задачи. И станции запускали? Хотя бы виртуально? Скажем, моделируя траекторию реальной станции, вроде "Луны-3". Для проверки? Если скажете, что так и было. И в реальности повторили траекторию "Луны-3" (или другой станции) только при помощи логарифмической линейки, и результатсошелся с опубликованными данными, то я действительно поверю, что расчет только на линейке возможен. Хотя и очень удивлюсь. Вы даже не представите насколько.
История "Планеты Бурь" http://shubinpavel.ru/




"Тише, горячие финские парни!"
Вы о разном. О действительно точной траектории, по которой можно запускать КА и даже без коррекций по пути попасть, куда надо - и о качественной оценке траектории и потребной для неё ХС.
Собственно понятно, почему пионеры астронавтики удовольствовались грубыми расчётами - им, скорее всего, было просто неважно; траектория как таковая была еще не нужна, доказывалась "теорема существования" - и не траектории даже, траектория в сущности нужна была для оценки нужной ХС, и вовсе не с точностью до сотни м/с. Они же все были не астрономы и баллистики, аналогично и фон Браун - ракетчик, а не математик. "Сколько там получается? Примерно 11 км/с, ну вот и ладушки, об остальном пусть у баллистиков голова болит, это их работа."
ЗыСы Считать ручками это конечно задолбались бы, но если бы кому-то тогда в 1900-1940 стало сильно интересно (и был бы ресурс) - могли бы, пожалуй, какой-нибудь аналоговый баллистический вычислитель состряпать, вместо того чтобы с арифмометрами и линейкой кувыркаться. Гидравлический, электрический, еще какой-нибудь Задача-то одна в сущности, на перебор траекторий.
Задача-то одна в сущности, на перебор траекторий.
Вы о разном. О действительно точной траектории, по которой можно запускать КА и даже без коррекций по пути попасть, куда надо - и о качественной оценке траектории и потребной для неё ХС.
Собственно понятно, почему пионеры астронавтики удовольствовались грубыми расчётами - им, скорее всего, было просто неважно; траектория как таковая была еще не нужна, доказывалась "теорема существования" - и не траектории даже, траектория в сущности нужна была для оценки нужной ХС, и вовсе не с точностью до сотни м/с. Они же все были не астрономы и баллистики, аналогично и фон Браун - ракетчик, а не математик. "Сколько там получается? Примерно 11 км/с, ну вот и ладушки, об остальном пусть у баллистиков голова болит, это их работа."
ЗыСы Считать ручками это конечно задолбались бы, но если бы кому-то тогда в 1900-1940 стало сильно интересно (и был бы ресурс) - могли бы, пожалуй, какой-нибудь аналоговый баллистический вычислитель состряпать, вместо того чтобы с арифмометрами и линейкой кувыркаться. Гидравлический, электрический, еще какой-нибудь
 Задача-то одна в сущности, на перебор траекторий.
Задача-то одна в сущности, на перебор траекторий.


Fakir> Вы о разном. О действительно точной траектории, по которой можно запускать КА и даже без коррекций по пути попасть, куда надо - и о качественной оценке траектории и потребной для неё ХС.
В том и проблема, что полет к Луне на минимуме скорости (причем в этот минимум входят и траектории облета Луны) настолько подвержен возмущениям, что без коррекций туда не долететь. Там отличия, буквально, в метры в секунду.
Вон выше я выложил кусок кривой попадания
Вот она
Так вот, для попадания в вершину нужна скорость 10841 м/с. То есть снаряд попадет в видимую часть Луны.
Для попадания в впадину нужна скорость 10843 м/с. То есть снаряд за чуть большей скорости пересечет траекторию Луны раньше Луны, после чего на возвращении попадет в нее.
Разница между этими траекториями (разных типов!) - 2 м/с!
Сравните с полной скоростью. И вспомните про точность логарифмической линейки. А если скорость будет на 1м/с больше или меньше, то при данном времени старта в Луну уже не попадем. Жаль гифку так не сделал.
В результате траектории без коррекции все с куда большей скоростью. Там да, попадание идет в вершину траектории и точности отработки импульса куда ниже. А скорость достижения Луны снижается с четырех суток, до полутра.
Fakir> Собственно понятно, почему пионеры астронавтики удовольствовались грубыми расчётами - им, скорее всего, было просто неважно; траектория как таковая была еще не нужна, доказывалась "теорема существования" - и не траектории даже, траектория в сущности нужна была для оценки нужной ХС, и вовсе не с точностью до сотни м/с.
В этом то и пролемма, почему-то все уверены, что важна точность в сотни метров в секунду. Хотя это дикая грубость. Даже метры в секунду уже важны.
В том и проблема, что полет к Луне на минимуме скорости (причем в этот минимум входят и траектории облета Луны) настолько подвержен возмущениям, что без коррекций туда не долететь. Там отличия, буквально, в метры в секунду.
Вон выше я выложил кусок кривой попадания
Вот она
Так вот, для попадания в вершину нужна скорость 10841 м/с. То есть снаряд попадет в видимую часть Луны.
Для попадания в впадину нужна скорость 10843 м/с. То есть снаряд за чуть большей скорости пересечет траекторию Луны раньше Луны, после чего на возвращении попадет в нее.
Разница между этими траекториями (разных типов!) - 2 м/с!
Сравните с полной скоростью. И вспомните про точность логарифмической линейки. А если скорость будет на 1м/с больше или меньше, то при данном времени старта в Луну уже не попадем. Жаль гифку так не сделал.
В результате траектории без коррекции все с куда большей скоростью. Там да, попадание идет в вершину траектории и точности отработки импульса куда ниже. А скорость достижения Луны снижается с четырех суток, до полутра.
Fakir> Собственно понятно, почему пионеры астронавтики удовольствовались грубыми расчётами - им, скорее всего, было просто неважно; траектория как таковая была еще не нужна, доказывалась "теорема существования" - и не траектории даже, траектория в сущности нужна была для оценки нужной ХС, и вовсе не с точностью до сотни м/с.
В этом то и пролемма, почему-то все уверены, что важна точность в сотни метров в секунду. Хотя это дикая грубость. Даже метры в секунду уже важны.
История "Планеты Бурь" http://shubinpavel.ru/




Copyright © Balancer 1997..2018
Создано 01.12.2017
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
Создано 01.12.2017
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
- Поиск
- Настройки
-
- Персональное
-
Здравствуйте, гость!
Гостевой функционал сайта ограничен. Для полноценной работы зарегистрируйтесь, пожалуйста.
- Тема
- RPG (самоуправление)
- Твиттер сайта Твиты пользователя @AirbaseRu
- Статистика
 Полл
Полл

 инфо
инфо инструменты
инструменты







 Wyvern-2
Wyvern-2

 Bredonosec
Bredonosec